Enrico Rinaldi
Research Scientist
University of Michigan
RIKEN Center for Quantum Computing
Theoretical Quantum Physics, Cluster of Pioneering Research
RIKEN iTHEMS
Profile
I am a Research Scientist at the University of Michigan.
I am based in Tokyo, hosted by the RIKEN Center for Quantum Computing (RQC) and the Theoretical Quantum Physics Laboratory at the Cluster for Pioneering Research at RIKEN, Wako. I am also a Visiting Scientist of the RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program, where I collaborate on projects in Quantum Computing, Cosmology, and Dark Matter theories.
My academic research is at the interface of computational and theoretical tools, applied to solving the mysteries of the Universe. Current projects span from using deep learning and quantum simulations to understand quantum gravity, to high-performance-computations of subatomic particles in theories that could explain the origin of matter.
I am working on projects related to low-energy nuclear physics, for example calculating nucleon-nucleon interactions or nuclear form-factors directly from the theory of Quantum Chromo-Dynamics (QCD). In addition, I study matrix models in the context of the gauge/gravity duality conjecture with the aim of understanding the possible intriguing relation between gauge theories and quantum gravity. In these projects I apply Machine Learning (ML) approaches to large amount of numerical data available from Monte Carlo simulations with the goal to make new and unexpected discoveries. Recently I also used quantum computing simulations to enable further discoveries on these matrix models.
My expertise is in Markov Chain Monte Carlo (MCMC) numerical simulations of quantum field theories, also known as Lattice Field Theory simulations, which use massively parallel supercomputers (CPU and GPU-based) around the world to solve the complex equations hiding the mysteries of particle physics. MCMC is also used in the field of parameter inference to compute the posterior probabilities of parameters involved in fitting a specific theoretical model to observational or simulated data.
In the past, I worked as an AI Researcher and Engineer at Arithmer Inc., a robotics and artificial intelligence startup in Tokyo, Japan. My research topics were focused around applications of 3D computer vision to enhance automatic measurements and decision making processes based on high-dimensional data. The importance of data and of the inductive bias of specific deep learning architectures were crucial to obtain functional models in these domains. I also worked as an Artificial Intelligence and Computational Physics consultant for other startups in Tokyo and as a teacher for Data Science Bootcamps at Le Wagon Tokyo (trying to inspire the future generation of data scientists!).
Download my resumé.
- Quantum Physics
- Particle Physics
- Lattice Field Theory
- Dark Matter
- Quantum Gravity
- Numerical Simulations
- Data Analysis
- Deep Learning
- Quantum Computing
-
PhD in Theoretical Particle Physics, 2013
University of Edinburgh
-
MSc in Theoretical Physics, 2009
University of Milan
-
BSc in Physics, 2007
University of Milan
Experience
Current and past affiliations
Research on quantum algorithms for quantum field theory, Projects are related to:
- Matrix Models
- Lattice Field Theories
- Variational Quantum Algorithms
- Quantum Information
Research on open quantum systems and combinatorial optimization, taking advantage of machine learning and quantum computing simulations. Projects are related to:
- Dynamics of OQS
- Matrix Models
- Graph Neural Networks for CO
- Scientific ML
- Simulation-based Inference
Working on state-of-the-art deep learning algorithms in 3D Computer Vision for robotics and computer graphics. Responsibilities included:
- Research
- Data exploration
- Model experiments
- Deployment
Skills
Obtain and analyze data to inform decisions. Probabilistic Inference. Descriptive Statistics. Time Series Analysis.
Simplify complex systems using models defined by mathematical equations. Algorithm development.
Python (PyTorch, TensorFlow, Keras), Julia, C/C++, Fortran
Excellent interpersonal skills. Team leader and team player. Outstanding presentation skills
Research
A brief overview of my research topics.
Since the early days of my life as a researcher, I have been interested in computational methods applied to physics. Before starting my PhD I performed research in Markov Chain Monte Carlo algorithms, first applied to statistical systems like corrugated surfaces (two-dimensional) and then applied to quantum gauge theories (four-dimensional), with ties to theories of gravity.
I expanded my physics reach during my PhD, studying gauge theories with extra dimensions and quantum field theories with scalars and fermions. Computational methods were still at the center of my research. In particular, I used Lattice Field Theory methods to investigate strongly-coupled theories which are not amenable to perturbative analytical methods. I was interested in gauge theories that could give rise to a particle similar to the Higgs boson, and that could extend our current knowledge of particle physics, currently summarized in the mathematically beautiful Standard Model.
During my first postdoctoral appointment, I continued exploring gauge theories with Higgs candidates, but I also started studying dark matter theories. Using numerical simulations of strongly-coupled theories, I investigated possible dark matter candidates that are tightly-bound heavy composite states, but also elementary dark matter candidates like the axion, which are very light. I also started an independent project about low-dimensional gauge theories connected to quantum gravity in order to test the holographic principle, also called gauge/gravity duality conjecture. The powerful computational resources used in this project allowed me to complete the best test of the holographic principle in 1 dimension, using numerical methods.
In my second postdoctoral appointment, I have started studying the properties of the neutron from the fundamental theory of its constituents, quarks and gluons. This theory, called Quantum Chromodynamics, can be solved using numerical Lattice Field theory methods but it requires the most powerful supercomputers in the world. One of the achievements is the calculation of the strength of interaction between the neutron and the weak gauge boson of the Standard Model. With an accuracy of 1% we can predict this strength directly from the equations of the fundamental theory, and this can reveal important signals of new physics when confronted with experimental results about the life of neutrons.
My current research topics are in the field of scientific machine learning, that is applications of artificial intelligence techniques to solve difficult physics problems or accelerate scientific discoveries. The complete list of my publications can be found on inspireHEP.
Accomplishments
Projects
Recent Publications
Some selected publications

We study the two matrix models using deep learning methods and quantum simulations. We benchmark the results against lattice Monte Carlo simulations.

The Hubble constant ($H_0$) tension between Type Ia Supernovae (SNe Ia) and Planck measurements ranges from 4 to 6 $\sigma$. To investigate this tension, we estimate $H_0$ in the $\Lambda$CDM and $w_0w_a$CDM models by dividing the Pantheon sample, the largest compilation of SNe Ia, into 3, 4, 20 and 40 bins.
Neural networks enable an important calculation in a popular approach to unifying quantum mechanics with general relativity
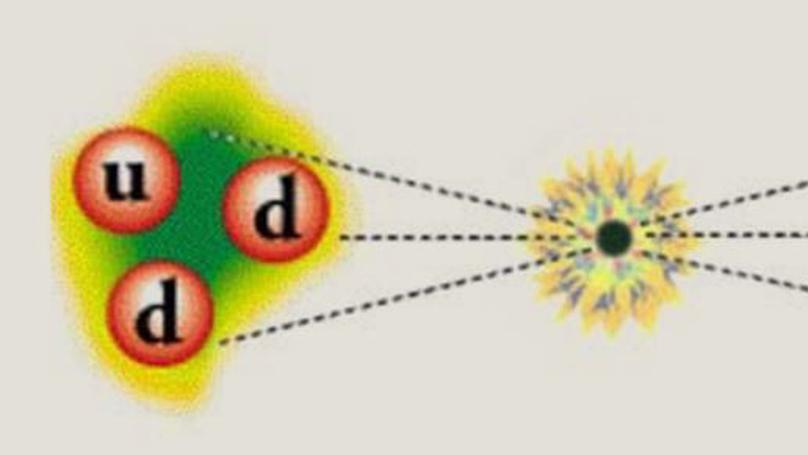
Fundamental symmetry tests of baryon number violation in low-energy experiments can probe beyond the standard model (BSM) explanations of the matter-antimatter asymmetry of the Universe. Neutron-antineutron oscillations are predicted to be a signature of many baryogenesis mechanisms involving low-scale baryon number violation. This publication presents first-principles calculations of neutron-antineutron matrix elements needed to accurately understand measurements of the neutron-antineutron oscillation rate.

We study the thermodynamics of the ‘ungauged’ D0-brane matrix model by Monte Carlo simulation. Our results appear to be consistent with the conjecture by Maldacena and Milekhin.
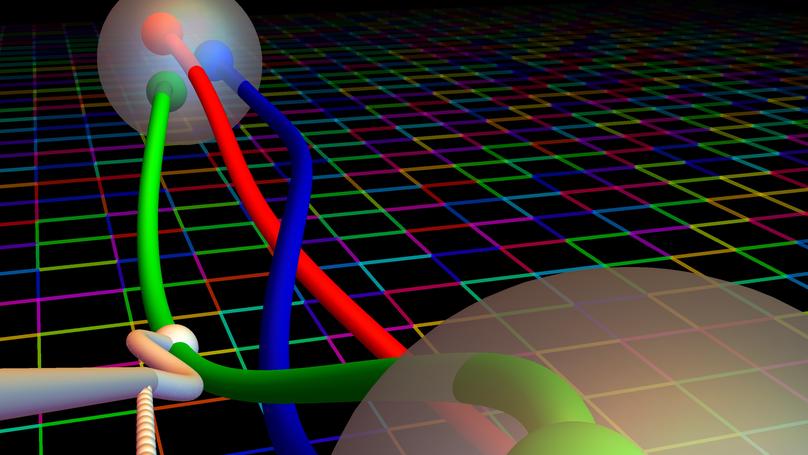
For the first time we directly calculate a fundamental property of the neutron from the equations of quantum chromodynamics without relying on experimental measurements. We reach a sub-percent precision, many years ahead of what was previously conceived, thanks to a new algorithmical improvement to reduce the stochastic noise in our calculation.
Recent & Upcoming Talks
Some featured talks and events